What Are Neural Nets?

Neural nets are systems that model the behaviour of the brain but it is neither as simple nor as complicated as that.

It is not that complicated because today's neural nets do not try and model the whole brain. The brain is made up of about one hundred-billion neurons with a square centimetre of the brain's cortex having about one million neurons with over one billion connecting fibres. The biggest neutral net made usefully so far, and it is a simulation, has only 8,100 neurons with either 417,700 or 1.2 million interconnections. This puts it at about an eight hundred-millionths of the size of the average human brain. Today's neural nets are trying to do very small specialised tasks and do not try to be as clever as a human.

Unfortunately it is also not that simple. To model neurons you first have to know how neurons work and this is difficult as they are very small and yet very complex. So what has to be done is model only the important parts of the neurons and their connections. Which are the important parts is not exactly known.

The development of neural nets has been closely connected to the investigation of the brain. Indeed some people today now try and see how the brain works by building neural nets and seeing how closely they match the brain when they operate.

Neurons

The diagram below shows an idealised electronic neuron,

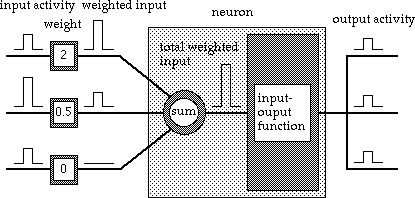
As can be seen there are a number of inputs, the number depends on how many other neurons there are and how interconnected the system is. Each input has a "weight" attached and the input coming into the neuron is multiplied by this. This weight could be zero therefore effectively shutting off the input. The neuron then totals the inputs and this total represents the neurons "activity level". This is then put through the input-output function to produce the output which either goes to a number of other neurons or to the output of the system.

There are three main types of input-output functions linear, threshold and sigmoid. A linear neuron's output is proportional to the activity level of the neuron. A threshold neuron's output is constant until a certain activity level is reached and then the output changes to a new constant level until the activity level drops back. A sigmoid neuron's output varies continually with the activity level but it is not linear, this is shown in the diagram.

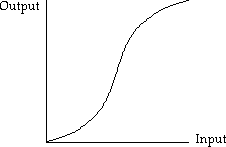
Sigmoid neurons are the most like real neurons but all three types must be considered rough approximations.

Connections

In each neural net there are many neurons. The simplest way to connect them up is shown below,

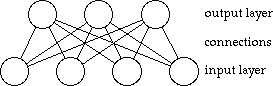
Information is put into the net by setting the activity of the neurons in the input layer. The net will then give the output it has been taught. The output is read by looking at the activity level of the neurons in the output layer. This system can be used to correct data as even if one of the input neurons is not given its data then the output will probably be almost the same as if the neuron had been given its data.

This organisation is, however, limited and today the commonest type of net has a third "hidden" layer.

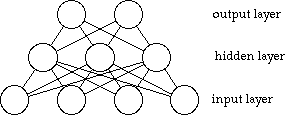
This allows the network to construct its own representation of the input rather than rely on just the patterns it is shown. It is also possible to have other hidden layers but this makes the network harder to build and teach.

Teaching is one of the major differences between computers and neural nets. With a computer someone has gone through and work everything out but to make a neural net work it has to be taught. The process of teaching a neural net adjusts the weights of the connections between the neurons. Interestingly when people first tried to analyse the weights in the network to try and find out how it works you get what has been called "connectionist glop" which is just as useful as trying to understand thought by disecting the brain. One of the main problems of neural nets has been how to teach them.

It is not just a matter of finding examples to give them or a person to work out the "correct" answer and tell the net whether it is right or wrong. To teach a neural net you have to decide which weights to change and by how much. To do this a number of "learning rules" have been made.

Learning Rules

Dating from 1949, the simple Hebbian learning rule increases weights whenever they are used, this ever includes when the task has already been learned properly. In 1960 this rule was changed by Bernard Widrow and Ted Hoff. This new Widrow-Hoff rule, also called the delta-rule, compares the observed performance with the desired performance to produce an "error signal", this is them used to strengthen or weaken weights. The engineering approach taken by these two has led to a learning mechanism that has worked in many real world problems such as filtering in high-speed modems.

A method used to increase the learning speed in neural nets is known as feedback. In this neurons in the output layer are connected so they feed information back to the hidden and input layer, the hidden layer can feedback to the input layer. Examples of such systems are now used in Ford Motor Co., General Electric, and other well-known corporations.

A learning rule developed for these systems by David Rumelhart and James McClelland is called the generalised delta-rule. It is based on the delta-rule but because of the extra hidden layers each layer has to be trained in turn. Unfortunately this rule can sometimes led to "dead ends" which can only be solved by randomising the weights.

Boltzmann Machine

In 1984 Geoffrey Hinton and Terrance Sejnowski developed what is known as the Boltzmann machine. This system has an input, output and a hidden layer. The output of each neuron is an all or nothing system but the input-output function is different. If the neuron receives a lot of positive inputs there is a high probability of it firing and a low probability if there are a lot of negative inputs. While learning the Boltzmann machine uses a simple Hebbian rule while being exposed to data. The data is then removed but some neurons keep firing even without data, an anti-Hebbian rule is then used. Decreasing the chance of something firing if it fires. This phase gets rid of the random effects of the connections themselves.

Simulation versus Modelling

Earlier I noted that the largest normal neural net was a simulation. This means it was not a network of model neurons that had been built but rather an ordinary computer was being used to simulate how the neurons would have behaved. This is one of the things I have said the computer is good at, simulation, but does this mean that no new technology will be needed but merely different programs for existing computers?

The answer is, no. There is a difference between model neurons and simulated neurons. Simulated neurons will never produce genuine intelligence, at best they will produce artificial intelligence. Model neurons on the other hand will be able to produce, eventually, real intelligence which happens to be man-made. The inability of computers to simulate neurons properly is connected with chaos theory, in that computers will always simulate things to a certain accuracy and then no more but a model will always be perfectly accurate and therefore better.

Another example of why computers will not be able to simulate all neural nets is seen in John Hopfield's work. He was investigating the difference between what he calls biological computation and the formal computation of computer programs. He noted that while computers have various mechanisms built into them to try and cope with faults, if they were presented with the error rates of a brain they would not even come near to coping. The brain can tolerate the death of millions of neurons without being disturbed. It is even possible, after recovering from massive damage, for it to reconstruct some of the lost information.

It is known that any system will try and settle to its lowest energy level. A soap bubble is a sphere because this is its lowest energy level. It is possible to design neural nets based on these laws, this approach is called "energy relaxation". If a soap bubble is hit it will wobble for a while before becoming a sphere again. If one of these neural nets is "hit", that is information is inputed, then the circuit will be pushed into a higher energy level. The network would then settle down into a energy minimum but these systems can be complex enough to have many minimal configurations so the system will be able to have more that one output. These systems cannot be modelled by computers.

Sleep and Dreaming

Many scientists think that when people dream their brains are going over information that has been received and optimising it. Some neural nets are now exhibiting the need for sleep and dreams. An example of such a net could be used to remember ten-digit numbers but it would only need two of the digits to recall the number. However the more examples it learned the longer it took to remember the earlier ones, also numbers were being remembered that had never been programmed but ones that could have been - a dream. If you map the circuits states as a three-dimensional energy surface where valleys are the remembered numbers. The dreams are slight depressions that have not been programmed. To remove them all the valleys were raised slightly to leave less room for the depressions. "Dreams" were then induced by adding slightly to the energy of the circuit to jog it out of these depressions. The net was then allowed to settle to a very low energy level, this was "sleep". After several of these sessions both problems disappeared.