Travelling Salesman Problem

Salesman's Job

For the first demonstration of the toolkit's power the purpose was to explore the workings of the toolkit rather than develop a new genetic algorithm. Several problems are well known in the genetic algorithm field, one of these is the Travelling Salesman Problem which is also a common test for other search space techniques. Because of this large sets of data readily available for test purposes with optimal solution already found by exhaustive search. As a bonus one of standard implementations is both simple and will exercise different toolkit components than The Blues.

The travelling salesman problem involves planning a route from city to city for a salesman to travel so that each city is visited once and only once apart from one city which should be both start and finish point. Additionally the total cost of travelling on the journey should be minimised. Another way to describing this problem is as finding the minimum cost tour among all permutations of the n cities in the salesman's itinerary. Although expressed in terms of a salesman travel plans this problem is equivalent to many other distance minimisation problems.

"Circuit board drilling applications with up to 17,000 cities are mentioned... , X-ray crystallography instances with up to 14,000 cities are mentioned... , and instances arising in VLSI fabrication have been reported with as many as 1.2 million cities.... Moreover, 5 hours on a multi-million dollar computer for an optimal solution may not be cost-effective if one can get within a few percent in seconds on a PC. Thus there remains a need for heuristics"

Johnson (1990)

These search spaces are often extremely large and any savings that genetic algorithms may give are very valuable.

Standard Decomposition

Although several genetic representations have been used for the Travelling Salesman Problem the path representation is both common and simple. In this the tour is stored as a list of n cities in chronological order. Evaluation is a matter of totalling the distances for each leg of the journey remembering to include the final trip back to the initial or home city.

With this ordered list representation comes the ordered crossover operator which is shown in Figure 10. Given two parents, p1 and p2, a subset of cities is chosen from the list. To create the first offspring p1 is copied and the selected subset of cites is reordered to match that found in p2. The second offspring is similar, a copy of p2 with p1's ordering imposed. A corresponding mutation is the order mutation operator which randomly selects two cities and inserts one before the other as shown in Figure 11.

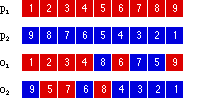
Figure 10 - Ordered crossover operator

Figure 11 - Order mutation operator

All other components in this algorithm's implementation are identical to those used by The Blues. This includes roulette wheel selection for both parents and a generational breeding model. Any fitness function is appropriate but in this case the unity class was reused.

Toolkit Performance

It is difficult to rate the first performance of the toolkit because many of the standard components had to be implemented in parallel with the algorithm. This does shows the extensible nature of the toolkit. There is no difference between the original construction of the toolkit and the construction of additional user components. Both just require simple objects to be inherited from the abstract classes provided. For this implementation of the Travelling Salesman Problem only a new evaluation class and main program body were required, ordered lists are part of the toolkit design.

Initial results were very promising. When the best individual was monitored during the algorithm it showed steadily lower costs with each generation. Unfortunately this value quickly dipped below the optimal cost solution defined for the test data. Investigation showed an error during the initialisation of individuals which allowed a salesman to stay in the same city for much of the time. After correcting this error results were still positive. Costs dropped slowly over the course of the genetic algorithm. Although the best routes were far longer than optimal route known they were shorter than the random routes which made the base population. A summary of the results can be seen in Figure 12, several of the optimum route segments have been found by the genetic algorithm. Other genetic algorithms implementations have performed much better than but here it was sufficient here to prove MUTANTS was capable of this implementation. Continued experimentation would have required more standard toolkit components to be built. Although any single component takes relatively little time to implement, making large numbers of them would have taken up precious time.

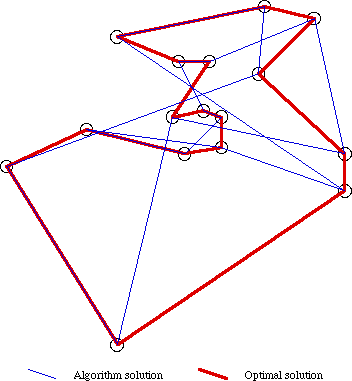
Figure 12 - Ulysses16 Travelling Salesman Problem