
Genetic Algorithms
Nature's Genetics
In the world around us there are millions of species each different from the next and within these species there are countless billions of individuals. All of this variety stems from the creation of life around three billion years ago. For over two billion years the most advanced organisms consisted of only a single cell. The structure and behaviour of each individual is controlled by a set of instruction called genes written in a four letter alphabet on long strands of DNA. Structures within the cell interpret these letters and then changes chemicals harvested from the environment into products for power, repair, or reproduction.
These single-celled organisms reproduce by fission, splitting into two components, each taking a copy of the DNA instructions. But the environment is hostile, ultraviolet light streams down from the sun and radiation seeps up from the rocks below. Occasionally letters in the instructions are damaged or the copying mechanism fails. The offspring has slightly different genes from its parents and there are new responses to the environment. Sometimes such individuals are failures, condemned by their genes. Sometimes they just cannot compete with their fellows for food. Most often they are little different from their parents but occasionally these changes, these mutations, make the individual better than its neighbours. Those who are better suited to the environment grow faster or survive longer and ultimately give rise to more offspring. These offspring would inherit any advantage and replace the parent type over a number of generations.
The process of species changing over time to become better at survival within the environment is called evolution. One advance that it produced was a new method of reproduction. Cells began to carry some of their genes in rings called plasmids. During meetings between individual they could exchange bundles, passing the environmental knowledge embedded within the plasmid from individual to individual. Successful plasmids spread amongst the population but unsuccessful plasmids encumbered their carrier who would die sooner and have less chance to spread the bad genes. Greater benefits came when certain genes came together that worked better in combination than in isolation. The likelihood of random mutation equipping one cell with both genes is low but with the crossover of genes between individuals these traits can arise separately and, once they become common in the population, join together within one individual.
From this soup of tiny creatures all the diversity of the planet has arisen, from roses to butterflies, mushrooms to mankind. Single cells have grouped together to form complex multi-cellular lifeforms. In these higher organisms genes are arranged in structures called chromosomes. Humans have 26 pairs of chromosomes, one of which is either an XX or an XY pair, the first pair for a female and the second for a male. This division of the species helps with the replacement for plasmid exchange used by simpler creatures. Two individuals each provide one half of the chromosomes needed to make up a complete set. Combining chromosomes is an opportunity to gain something better for their offspring. Deficiencies in one parent can be made up by the corresponding genes from the other parent. Like any other animal humans try to select a successful mate to get the best chance of survival for their child.
At the change over from single celled to multi-cellular forms there was a rapid period of development and diversification called the Cambrian explosion. A huge range of species appear but most have no living relatives today. Although they were well equipped for life they did not survive. Perhaps they had disadvantages compared to others but maybe they were just unlucky. Such die backs are common throughout history. The dinosaurs lived on Earth for about 150 million years before their extinction around 65 million years ago. One reason given for their extinction was the impact of a asteroid in the area which is now Central America. Devastation and destruction followed but more importantly disruption to the environment. Animals that had done well died out unable to adapt fast enough. In a geological instant half of species on the planet were wiped out. This is just one example of the many mass extinctions our planet has suffered. With each such event the diversity of life is devastated and will never return to the same extent.
Evolution is the aggregation of thousands of semi-random events and the natural pressure to reproduce or die. This has been compared to climbing a mountain. Starting at the bottom a species rises up through ever fitter forms. There is no going back and those who try will die. A species cannot even stop upon reaching one of the mountain peaks because these mountains are not constant. The ever changing physical and biological environment determines what is good and bad for each generation and with this mountains slowly rise and fall. Every species must continually search for perfection and in so doing will change what is perfect for those around it.
Computational Genetics
Problems can often be simplified to the search for an optimal solution through a range of possible solutions. Such search spaces can be huge and an exhaustive search would take an unrealistic time even with the fastest computers. Simple problems may have linear time complexity. A problem of size 10 will take twice as long as a problem of size 5. Intractable problems can have factorial time complexity. A problem of size 10 will take 10*9*8*7*6 times longer than a problem of size 5. Figure 1 shows the time taken to solve linear and factorial time complexity problem on the same computer. Such intractable problems must therefore be solved by pruning away or ignoring most possibilities.
| Problem size | Linear time | Problem size | Factorial time | |
|---|---|---|---|---|
| 10 | 0.0001 seconds | 10 | 0.36 seconds | |
| 100 | 0.001 seconds | 20 | 7714 years | |
| 1000 | 0.01 seconds | 30 | * | |
| 10000 | 0.1 hours | 40 | * |
* indicates times greater than age of the universe
Figure 1 - Time Complexity
Artificial intelligence problem solving strategies fall into two categories - strong and weak method. A weak method makes few assumptions about the problem domain and hence is portable to other areas but little pruning is done and time scales grow rapidly for large problems. A strong method avoids this by making major assumptions about the problem domain but it may require significant redesign when moved to even a closely related problem. In between these two extremes genetic algorithms can be tuned to become strong or weak, either widely applicable or problem specific. Aspects of genetic algorithms can be seen in a number of other weak search techniques.
Randomly generating many solutions to a problem is usually simple. Each solution can then be evaluated and given a score according to its success. Call routing solutions are just lists of connected exchanges, these could be randomly assigned. Evaluation involves adding up the workload at each exchange. Positive scores for under capacity exchanges and penalty points for overworked ones.
Hill climbing is a more directed approach similar to a specie's climb up the mountains of fitness. Starting with a single random solutions and mutate slightly, swapping a single exchange. Perhaps generate a few more variations to get an idea of the locale area. Then pick the solution with the highest evaluation and start mutations again. Evaluations will rise until a optimal solutions is found. However, this may not represent the global optimum but rather a local peak with higher values to be found elsewhere. To increase the chances of finding these continue with a new random solution and hope for a better final solution.
Simulated annealing introduces chance into its climb to avoiding the traps of local optimums. An identical random start and mutation but the best evaluation is not always selected. The probability of choosing a new solution is a function of both old and new evaluations and an additional parameter T known as the temperature. Initially the temperature is high and so is the probability of selecting a new solution independent of its evaluation. This continues until the system reaches some sort of balance with little more progress being made. The temperature is lowered and it is allowed to settle again closer to the optimum peak. At a temperature of zero the system acts like a hill climber to find the locale and hopefully global optimum.
John Holland was the first to apply additional natural principles to problem searches. Within a population of random solutions crossover occurs between individuals occurs. Such combinations can bring together successful attributes making increasingly better solutions. Since their introduction genetic algorithms have been employed on a variety of search space and optimisation problems including call routing, job scheduling, and database query optimisation.
Genetic algorithms are derived from the field of biology and much of the terminology has been borrowed. A solution is know variously as an individual, a structure, a genotype, or a string. Sometimes chromosome is used as an alternative but this is misleading as some individuals could contain several chromosomes. Chromosomes are sequences of genes, also called features, characters, or decoders. Fixed positions within the chromosome which hold particular characteristic are loci and the values that might appear are alleles or feature values. Finally data within an individual is its genotype but the meaning of this representation as defined by the user is its phenotype.
Basic Algorithm
Genetic algorithms have six basic steps in common. The Blues is an artificial problem manufactured to illustrate these. Possible solutions to the problem are the integers from 0 to 255. Each integer represents one of four colours: red, blue, purple, and black. Success for the algorithm is measured in the number of blue solutions found in comparison to other colours.
First, a set of potential solutions must be initialised to form the starting population. To represent numbers in the range 0 to 255 a random 8-bit binary vector is used. Figure 2 shows a selection of individuals from the population. Every number has a corresponding colour picked by a secret function (which examines the first two bits of the binary representation).
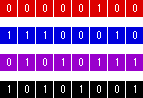
Figure 2 - Random population
Second, each solution is evaluated according to its fitness, in this case its colour. Blue is given priority and scores 10. Lower scores are for solutions further down the mountain of fitness - 5, 3, and 2 are given to red, purple and black respectively.
Third, new solutions are created using mutation and crossover on the current population, typically with more crossover than mutation, say a 3:1 ratio. Conserving and combining features is generally more helpful than varying them. A mutated descendent will differ from its parent in only a single bit as seen in Figure 3. Crossover requires two parents and produces two offspring. Select a random point along the binary vector and split each parent at this point. Then exchange the tail sections of each vector to produce the offspring shown in Figure 4.
Figure 3 - Mutation operator
Figure 4 - Crossover operator
Selecting those individuals to breed requires some element of chance. In nature some animals are lucky and some unlucky but those with better genes reproduce more. Genetic algorithms allow more offspring from high scoring individual than from low scoring individuals. A technique called roulette wheel selection has a probability of choosing an individual proportional to its evaluation. The Blues uses this to select the primary and, if necessary, the secondary parent for reproduction.
Fourth, room must be made within the current population for the new individuals. Here the entire population is removed.
Fifth, the new solutions are evaluated using the 10, 5, 3, 2 scoring system and inserted into the population.
Sixth, if there is no more time then stop, otherwise go back to step three and make some more individuals.
From a random start the roulette wheel picks out more blue individuals than other colours. If mutation makes an offspring then there is only a 2 in 8 chance that a colour change will take place. If crossover is used then there is only a 1 in 7 chance that the crossover point will be between the first and second bit, no other points can affect the offspring colour. Even if that point is chosen the other parent would have to differ in the second bit to produce a change. From this and the 3:1 crossover-mutation ratio it can be calculated that there is only a 13 in 122 chance (about 11%) of a blue individual giving rise to a non-blue offspring. With each generation more blues will be picked and most will stay blue. Other colours are also resistant to change but are picked less often. As can be seen from Figure 5, blue wins on average. Each dot is an individual and each column a population so the change from left to right represents the evolution of the population. The population is never totally blue because these probability predictions only work well for very large populations. In small populations of 32, as below, chance may result in another colour being predominant.
Figure 5 - The Blues
For those with a Java capable browser Figure 5 shows an animated version of The Blues. Starting with a random population the applet goes through all the stages above. Clicking on the applet will bring up a panel which controls various parameters used in the genetic algorithm. Try increasing the crossover rate and decreasing the mutation rate, the banner becomes almost all blue. Mutation tends to bring variety to the population and crossover tends to bring homogeny. Evaluations of the various colours can be changed to select for a different colour or to make finding the best colour harder. If you want to use larger populations or have more generations then the block size should be reduced. If you are interested source files are also available - World.java, Chromosome.java, ControlFrame.java.
In summary the steps of a genetic algorithm are:
- Initialise population with individuals
- Evaluate each individual in the population
- Create new individuals by mating between those in the population; apply mutation and crossover as the parents mate
- Delete members of the population to make room for the offspring
- Evaluate the new individuals and insert them into the population
- Stop if time is up, otherwise go to 3
Classic genetic algorithm components are shown in The Blues. A binary vector used to represent integers was the first ever genetic algorithm representation. Initial solutions were generated with random binary initialisation which fits almost any circumstance. Evaluation technique are normally unique to an algorithm but in many instances decoding produces numbers and mathematical functions are then applied. Reproduction is with single bit mutation and single point binary crossover. Deletion of old and insertion of new individuals is often treated as a single process with one name. A generational model creates an entirely new population for each cycle.
Genetic Theory
Current mathematical theory for genetic algorithms is based on a binary vector representations. The notion of a schema is introduced, a template made of 1's, 0's, and *'s. A schema represents all strings which match it on all positions other than *.
Consider the schema (11******) which matches 64 strings including
(11000000) (11111111) (11010101)
It would also match all blue solutions from The Blues. Every schema matches 2r vectors, where r is the number of * symbols in that schema. The order of a schema is the number of fixed positions, i.e. the number of 0's and 1's. The defining length of a schema is the distance between the first and last fixed position. These are written o(s) and d(s) respectively, for example:
S1 = (***001*110), o(S1) = 6, d(S1) = 10 - 4 = 6 S2 = (****00**0*), o(S2) = 3, d(S2) = 9 - 5 = 4 S3 = (11101**001), o(S3) = 8, d(S3) = 10 - 1 = 9
A schema's order proves useful in calculating the survival probabilities under mutation and the defining length can be used similarly under crossover.
A few simulations or a bit of mathematics will show that an above average schema gives rise to an exponentially increasing number of offspring in future generations. Further, low-order schema are more likely to survive the recombination process of crossover. From this work has come two theories:
Schema Theorem - Short, low-order, above-average schemata receive exponentially increasing trials in subsequent generations of a genetic algorithm.
Building Block Hypothesis - A genetic algorithm seeks new-optimal performance through the juxtaposition of short, low-order, higher-performance schemata, called the building blocks.
For a more detailed explanation and proof of these theories see Michalewicz (1992).
Vector Representation
Vectors, also called strings or arrays, are sequences of values all belonging to the same type. Bits, or booleans, are a typical choice but integers, real numbers, or complex structures are equally valid.
With the common binary vector representation comes a number of genetic operators for mutation and crossover. Single bit mutation and one point crossover have already been described. Multiple applications of these operators can give rise through a number of generations to any possible recombination of an individual but most would be stopped in the first generation. There are several crossover operators which provide a more diverse mixing of genes. Two point crossover chooses two random points and exchanges the central section of between individuals. Multi-point crossover extends this to a fixed arbitrary number of point pairs. Segmented crossover works with random number of point pairs. Shuffle crossover first randomly permutes the binary vector, applies another crossover operator, and then reverse permutes the vector.
Although flexible binary vectors have their limitations. To represent 100 real numbers in the range -500 to 500 accurate to the 6th decimal place would require 3000 bits. Such a long vector gives a search space of 101000 possibilities. Different representation can be chosen to help the genetic algorithm, say a vector of floating point numbers. Specific mutation and crossover operators are needed for this representation. Random mutation replaces old numbers with new ones chosen from a specified range and random creep adjusts each number up or down by a small amount. Crossover can work in the same way as binary representations or can combine two numbers as an averages.
With the introduction of specified ranges for numeric values reproduction operators may drive an individual outside these ranges. Such individuals represent an impossible or illegal solution. Careful design of operators can prevent this but it is not always possible. One option is to assign a penalty to the individual during evaluation. Selection pressure could then drive out these poorly formed individuals. On the other hand these individuals may have evaluations high enough to overcome this penalty and the population would become crowded with unusable individuals. A more computationally intensive option is to repair the individual, removing its illegal features to produce the closest legal alternative. This can defeats the purpose of a reproduction operator if the final individual looks nothing like its parents.
Messy Representation
In nature individuals carry redundant or duplicate information, such as multiple copies of genes, or paired chromosomes. This is an important feature of nature's robust designs. Messy genetic algorithms copy this, allowing redundant or even contradictory genes. A real number vector shows how this is done (0.1, 0.2, 0.4, 0.8) is encoded as ((1, 0.1), (2, 0.2), (3, 0.4), (4, 0.8)). Each value has been replaced by a (position, value) pair. Other alternatives include: reverse order ((4, 0.8), (3, 0.4), (2, 0.2), (1, 0.1)), duplicates ((1, 0.1), (2, 0.2), (3, 0.4), (4, 0.8), (4, 1.6)), and omissions ((1, 0.1), (2, 0.2), (4, 0.8)). Vague representations have to be evaluated with some default values and arbitration between conflicting values.
Only two crossover operators are required - cut and splice. The first breaks one individual into two less specified individuals. The second joins two individuals into one more specified individual.
Improved Initialisation
Nature never starts with a clean sheet, new problems are always met with modifications to previous solutions. Following this lead genetic algorithms can start with non-random populations. If an initial population of 100 individuals is required then randomly generate 500 and pick the best. Starting with these solutions is likely to speed up the genetic algorithm's search but could also hinder it in finding less obvious but higher scoring solution.
In an effort to cover the search space completely solutions can be chosen to be as diverse as possible. Generating this diverse population will take extra time. But by preventing any bias in the initial population the genetic algorithm has its best shot at finding the optimal solution.
Sometimes good results can be achieved by combining genetic algorithms with existing systems to produce hybrids exhibiting the best behaviour of both. The previous system starts by quickly generating a number of good solutions. These can be fed into the genetic algorithm as the starting population, hopefully concentrating the search to a more productive area.
Competitive Fitness
Evaluation functions try to score a representation fairly by what it can achieve, nature rarely does this. Instead examinations are competitive with little hope for the losers, no matter how good. Genetic algorithm's equivalent are fitness functions. After all individuals have been evaluated they pass to a second stage where their evaluations are compared against each other. As usual there are several different fitness techniques that can be applied, only some are mentioned here.
Windowing works on the basis of a certain minimum requirement. All individuals will have this amount removed from their initial evaluation. In this smaller range of positive values the differences between individuals are emphasised. What amount to remove must be decided, perhaps some fixed minimum score, perhaps equal to the minimum evaluation present, or some more stringent value.
In addition to emphasising differences fitness functions can reduce them. Linear normalisation ranks all individuals' evaluations, 1st, 2nd, 3rd, and later places are awarded. For 1st place the reward is a larger but not overwhelming share of the offspring. This prevents a single high evaluation individual from producing the lion's share of offspring in the next population. If this does happen important genes can be lost and never recovered. Those in lower places are rewarded less, and those in last place may receive nothing at all.
Breeding Techniques
Previous sections have looked at specific pieces which make up genetic algorithms but the broader picture has been ignored. These pieces must be pulled together by a breeding techniques such as the generational model used in The Blues. Before examining other models a few general parameters should be considered.
Population size, for instance, can have a great affect on the performance of the genetic algorithm in more ways than one. Choosing a small population size reduces the possible diversity of individuals and may well lead to sub-optimal solutions. Choosing a large population size will slow the algorithm down as there are more individuals to deal with and each generation will take longer.
With the selected reproduction operators there must also come the relative importance of each. Mutation explore new possibilities but can be destructive as well as creative. Crossover is safer, working with pre-existing building blocks, but if an important characteristics is lost it is never recovered.
When should a genetic algorithm stop? It may be when there is no more time and an answer due. Perhaps a certain number of generations has always proved sufficient in the past and so it seems appropriate to stop then. If a solution is required with a certain minimum evaluation then the best individual from each generation can be compared against it. When there are no other outward criteria with which to make the decision it is best to stop a genetic algorithm when the majority of the population has converged towards a single answer and no more progress is being made.
The generation model sometimes suffers from the loss of the best individual through chance, particularly when the population size is small. An elitist component can be added to several models to prevent this. Before normal reproduction begins a copy of the best individual is made and transferred to the new generation to guarantee a continuation of its line.
An alternative mechanism to achieve the same effect is to replace a generational with a steady state model. Here only a few new individuals are generated at a time. Now it must be decided which individual should be replaced. One particular alternative called prelection compares offspring with their parents and choose the better individual. Or the choice can be made randomly, the only selection pressure will be that provided by parent selection. Or the worst individuals in the population can be chosen. Another technique which goes particularly well with the steady state model is the imposition of a duplicate individual ban. No newly created individual may be the same as any other existing individual. It is computationally expensive to perform all the comparisons but a good way to ensure diversity within the population.
This only scratches the surface of modelling techniques available. Here are quick summaries of a few more.
- Inbreeding - crossover within small populations to emphasis good traits.
- Crossbreeding - crossover between diverse individuals to combine different traits.
- Multi-criteria sub-populations - separate populations with different evaluation functions, occasional crossbreeding between populations.
- Co-evolutionary systems - several parallel genetic algorithms whose evaluation functions are interdependent.
- Mating template - mating only permitted between individuals of the same type.
| Introduction | Toolkit Design |
| About this site | Mutants | © Matthew Caryl |